A Critical Essay on the Classic 1917 Tome by D’Arcy Wentworth Thompson
Originally Anthologized in the 2002 Volume of the College Text
Nonfiction Classics for Students,
Published by the Gale Group.
Marjorie Partch is a Jungian astrologer, writer, and graphic designer. In this essay, she considers Thompson’s interdisciplinary approach to the theory of evolution in contrast to Darwin’s.
When the Scottish classicist, mathematician and naturalist D’Arcy Wentworth Thompson [1860 – 1948] wrote On Growth and Form in 1917, Darwin’s theory of evolution was not only relatively new, it was at the height of intellectual fashion, certainly within the scientific community if not with the religious community. Thompson’s highly original thesis on morphology — the branch of biology that examines the forms and structures of living organisms — dared to question the principle of an ever-upward, magically directed, ascending spiral toward perfection that Darwin had put forth as the notion of Natural Selection in his seminal work, The Origin of Species, in 1859. Where Darwin draws frequent analogies from Nature to a cow-breeder culling his herd, Thompson sees the physicist’s underlying harmony of cause and effect; he sees energy interacting with matter in mathematical terms.
If Thompson’s work was regarded as controversial in its own time — because it first of all questioned, and then largely ignored, this prevailing assumption of an inevitable progression toward a supposed ideal — today his work seems nothing less than heretical. Or refreshing, depending on one’s point of view.
Nowadays, Thompson’s audacity is all the more striking, particularly as his challenge to Darwin comes from the scientific, and not the Creationist, quarter. Thompson, while not denying the Divine Mystery as the absolute final cause, also does not deny the phenomenon of Natural Selection. He simply points out that this process of elimination of the unfit, of unsuccessful forms, need not imply teleology — that is, a purposeful development or design toward a final end. To dispute this ingrained notion of a purposeful progression to evolution, was then and remains now quite a radical break with the prevailing thinking about Nature.
But, we may ask, aren’t all the changes over time in organic forms, after all, improvements in structure better suited to meeting challenging changes in the environment? The answer is, actually, No, not necessarily. In fact, while most adjustments in form were at one point in time advantageous to the organism, many of these features have become obsolete. These “leftovers” are simply lingering on past their functional purpose, and have not been “cleaned up” after their usefulness has expired. There are also many failures in mutation, many “wrong turns” down blind alleys. It is Thompson’s contention that this philosophical interpretation of progress becomes a dogma. This then blinds the naturalist to the more immediate causes for “fortuitous variations” in form: the interplay of physical forces with geometric structures.
Thompson maintains that we do not need to look quite so far afield from the core duality of force and form to learn more about changes in form, whether in terms of the growth of an individual organism or part of an organism, or whether we are looking at evolutionary variations within a species over time. Feeding the doctrine of teleology — the assumption of steady upward movement toward Nature’s presumed magnum opus of the frontally lobed, opposably thumbed, bipedally superior Homo sapiens — starves the scientist of the empirical observation of the direct mechanical causes of adaptation and changes in form. The fundamental mechanics of growth and change in form tend to be overlooked. They can be explored, quantified and described in mathematical detail, furthering our understanding of morphology.
Thompson Opens his Introduction with these words:
“Of the chemistry of his day and generation, Kant declared that it was a science, but not Science, for that the criterion of true science lay in its relation to mathematics … A hundred years after Kant, Du Bois Raymond declared that the chemistry of the future must deal with molecular mechanics by the methods and in the strict language of mathematics, as the astronomy of Newton and Laplace dealt with the stars in their courses …”
[On the mathematical definition of form]:
“We are brought by means of it in touch with Galileo’s aphorism (as old as Plato, as old as Pythagoras, as old perhaps as the wisdom of the Egyptians), that the book of nature is written in characters of Geometry.”
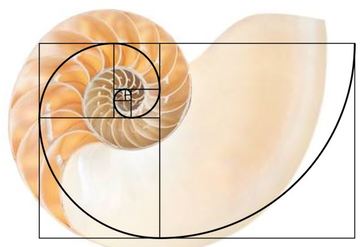
Thompson sees the application of physics and mathematics to the field of zoology as no less an occasion for awe in the face of natural phenomena than the prevailing teleological assumptions. He feels his approach enhances an even deeper appreciation of the intricacies of the ultimate mysteries of life. Thompson expresses his love of Nature and wonder at its mysteries in such poetic terms that this has been called as much a work of literature as a work of science. It could also be called an extended meditation on the mathematical patterns inherent in nature everywhere, from the inorganic crystalline structures of snowflakes to the spirals in a nautilus shell to the curves of a living and growing ram’s horn.
While some may recoil from the “mechanization” of the living body of Nature, who can resist the engineer’s delight in the design of a bird’s wing? But Thompson can hardly be accused of reductionism when he muses on “the shape of a snail-shell, the twist of a horn, the outline of a leaf, the texture of a bone, the fabric of a skeleton, the stream-lines of fish or bird, the fairy lace-work of an insect’s wing.” These are no less beautiful under closer examination, and he intends no slight when points out that “no organic forms exist save such as are in conformity with physical and mathematical laws”— and demonstrates that all these wonders can be described mathematically. For Thompson, “Numerical precision is the very soul of science.”
He elaborates:
“To seek, not for ends but for antecedents is the way of the physicist, who finds ‘causes’ in what he has learned to recognize as fundamental properties, or unchanging laws, of matter and energy. In Aristotle’s parable, the house is there that men may live in it; but it is also there because the builders have laid one stone upon another. It is as a mechanism, or a mechanical construction, that the physicist looks upon the world; and Democritus, first of physicists and one of the greatest of the Greeks, chose to refer all natural phenomena to mechanism and set the final cause aside.”
Throughout On Growth and Form, D’Arcy Thompson’s unique perspective as a triple scholar is called into play. His fully professional background within each discipline does more than just add to the others —there is a blending between them. They have been “chemically combined,” to create a new alloy. His grounding in Classics and Mathematics assures that he has read (even translated) not only Plato and Aristotle, but Archimedes, Euclid, Pythagoras, et al. He brings the full depth of his decidedly Greek sensibility and insight to bear on his astute observations of Nature. Thompson was not only a modern Renaissance Man, he was an embodiment of one of his favorite principles — Synergy: “The interaction of two or more agents or forces so that their combined effect is greater than the sum of their individual effects.” This is exactly the cumulative effect of his arguments. They combine to form a perspective as multifaceted as one of Thompson’s beloved dodecahedrons (a 12-sided geometric figure).
Each chapter takes a small question of form, and examines it from one angle and then another, and then another, in much the same way that Bach introduces a simple melodic phrase, which is then amplified and extended and interpolated by various instruments. Various points invite reciprocal counterpoints. A certain tension escalates in the call and response. And then there is an explosion, as the individual elements come together and develop their own dance, and a full fugue emerges.
We need not anthropomorphize a celestial engineer working out the immediate advantages of hollow-boned birds’ wings with a slide rule and protractor. The laws of Nature, Divinely inspired, do that … naturally. The solid-boned birds, whose more rigid, heavier wings weighed them down or which snapped in the wind, were eliminated from the gene pool, allowing the hollow-boned specimens to thrive and multiply. Thin, cylindrical tubes, by the very nature of their shape, tend not to buckle — under their own weight or under external loads or pressures, such as wind. 
Thompson celebrates the success of this model in a detailed mathematical contemplation of the interplay of forces and stresses in the air pressure working “against” the wing, and the structural resistances and advantages in the actual construction of the wing. He illustrates his points with ancient and recently discovered ratios and formulas in such a way as to suggest that the aerodynamic circumstances themselves, interacting with the developing organism, gave rise to the wing’s design. Similarly, the strength of a tree is directly related to the wind-pressure it must withstand.
Thompson gives a hilarious and informative example of this subtle principle in his exposition on honeycombs. There was much impassioned discussion at his time of writing concerning the marvel of the bees’ ingenious economy in employing their famous hexagonal shape. There was some debate as to whether it was the bees’ own intelligence which devised this architectural plan, or whether it was Divine instruction guiding their instincts. But everyone agreed, including the mathematicians, that the hexagonal shape afforded the absolute most efficient use of space within the hive, and the most economical use of wax in the construction of the cells. There was much specious comparison of “ideal angles” (110deg and 72deg), with impossible “measurements” of the bees’ roughly hewn angles, but they did come close enough to warrant general amazement.
However, Thompson observes that along the outside edges of the hives, the cells are round, and not hexagonal at all. In other words, when the cells of the hive are not adjacent to other cells, they do not assume the shape of a hexagon. He further observes that as the bees are working, they are not creating flat edges to the sides, but rather, simple rounded out hollows or cylinders. The tubular cell walls only become flat, by default, as neighboring bees scrape down adjacent walls to a final degree of thinness, each working to maximize the interior area of his cell, pushing up against the adjacent cells of his neighbors.
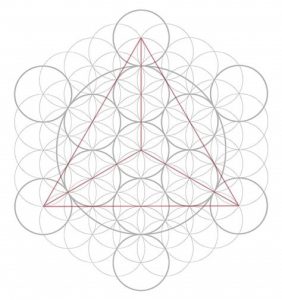
Thompson drives his point home with the observation that when soap bubbles, for that matter, are amassed together, their spherical shape tends to distort and collapse into flat edges where the bubbles’ walls meet. He concludes his discussion of this subject with the simple fact of geometry that a circle can be surrounded by exactly six circles of similar size; and hence any natural circular or spherical cluster flattens into a hexagonal honeycomb shape, be it soap bubbles or living cells … or honeycombs — provided the material with which they are constructed is pliable enough. 
It is a necessity of physical law; geometric, mathematical law, that they assume this shape. In short, honeycomb cells are hexagons because they have to be. Actually, flat circles become hexagons, but spheres become dodecahedrons. We can observe the same “packing” phenomenon in crates of oranges or the compressed, faceted flesh of pomegranate seeds. This has far more to do with intrinsic physical dynamics such as surface tension, and matter interacting with forces (such as mutual pressure and weight), than with the mysterious motives and causes, immediate or final, behind insect behavior. This is but one example of why it is important for naturalists to take physics and mathematics into account. This is a very clear and simple illustration of what Thompson means when he asserts that the form of an object is a “diagram of forces.” 
The object or organism’s shape is like a footprint in the sand, tracing where and how various forces have acted, or are acting, upon matter. The organism’s own process of growth is one such force. That genetics enters the dialogue between force and matter, such that fetal development anticipates environmental stresses, does not detract from Thompson’s argument that force determines form. That is simply Nature’s pre-emptive prerogative at work to accelerate the process of adaptation.
This view also need take nothing whatsoever from our wonder at the mystery of Creation, or the notion of a design or purpose to it. It may not bring us any closer to knowing what that purpose might be, but it certainly doesn’t preclude the question. If anything, we are privileged to glimpse the implicate order at an even deeper level of the overall design. This view only enhances our appreciation of Nature’s creativity:
“The harmony of the world is made manifest in Form and Number, and the heart and soul of all the poetry of Natural Philosophy are embodied in the concept of mathematical beauty.”
Thompson is fond of quoting Kant, who says:
“It is Nature herself, and not the mathematician, who brings mathematics into Natural Philosophy.”
Matter as Diagram of Forces is the introduction of a theme that Thompson builds into a brilliant fugue in his chapter on ratio in logarithmic spirals. What more Greek a concept is there than Ratio? And this theme interweaves, warp to woof, with his earlier theme of geometric Necessitas.
Thompson seems to delight in presenting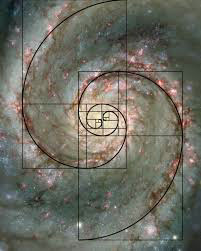 
ratios throughout the text. He begins with the simple. The ratio between the thickness of a stalk of grass to the stress of its own weight is a square; but aha, its length to its weight? Cube. This he readily correlates to bone mass and body weight in animals. Gradually he builds to one of the most elegant, and prevalent, ratios known to exist throughout Nature. Sometimes called, after Euclid, the Divine or Golden Section, it is also known as the Fibonacci series. Expressed as a ratio,
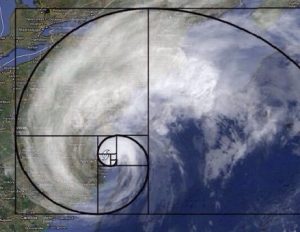it is roughly 3:5. Expressed mathematically it is a recursive sequence: 1, 1, 2, 3, 5, 8, 13, 21; each value is the sum of the previous two. Expressed geometrically it is the spiral that makes a nautilus shell a nautilus shell. Each chamber within the nautilus shell equals its two predecessors in size. We see exactly this type of growth throughout not only seashells, but animal horns, and with an added corkscrew twist, in the interval between leaves on a stem; even in galaxies and storms. By mathematical necessity, this spiral occurs wherever growth occurs in this 3:5 ratio. And this growth ratio occurs throughout Nature.
It is perhaps here that we can best see the signature of Nature Herself, signed with a flourish.
— C.G. Jung
Notes
https://www.theguardian.com/books/2017/jul/21/growth-form-darcy-wentworth-thompson-review
Marjorie Partch is a counseling, teaching, and writing Jungian astrologer and Tarot interpreter with more than 35 years’ experience. In addition to her training in transformational astrology, she has studied Integrative Therapy with an emphasis on the work of C.G. Jung, and is a longtime student of yoga, meditation, and Kabbalah, as well as a practicing artist and poet. Marjorie was a contributor to Your Birthday Sign Through Time, Simon & Schuster, 2002. Transplanted from her native New York City in early 2001 (by way of Vermont), she is now happily available in Fairfield County. Ordained in 2006, Marjorie received her labyrinth facilitator training from Lauren Atress in the same year, and shares her Blue Lotus canvas labyrinth as a tool for spiritual transformation and Sacred Activism. Marjorie also offers Reiki sessions in conjunction with or apart from spiritual counseling, with or without the tools of astrology or Tarot; in person or by Zoom or by phone: (203) 286-7525 / https://AlephTalks.com/Astrology.